
Remember that when using a scatterplot, the idea is to understand how the response responds to changes in the predictor. How many books were in this shipment? (a) What has Caitlyn used as the predictor? What about the response? (d) One of the shipments weight a little less than 7 pounds.
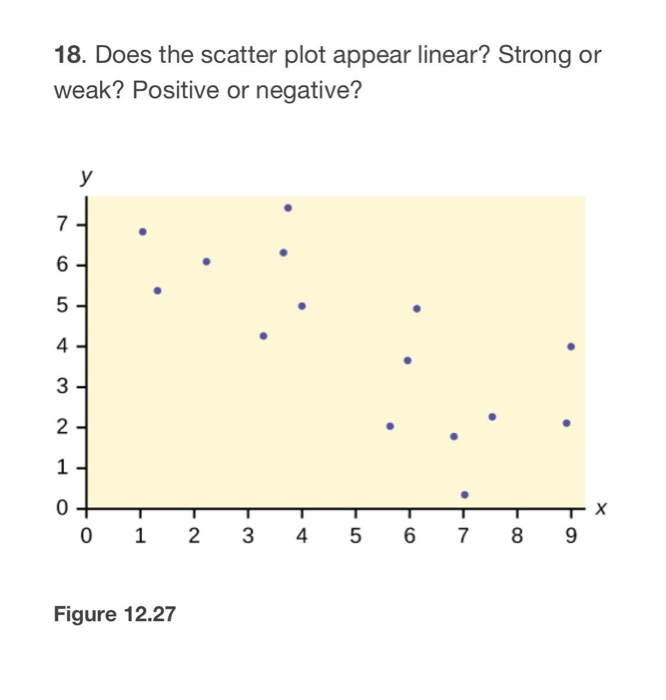
(c) What was the heaviest shipment Caitlyn made? (b) Describe the association between the two variables. (a) What has Caitlyn used as the predictor? What about the response? Use this scatterplot to answer the following questions. She plotted the data in the scatterplot below. In order to better predict her costs, she has been collecting data on the number of books in each shipment she has sent and the weight of the shipment. ExampleĬaitlyn has started a business selling textbooks and novels online. For scatterplots with linear patterns, the correlation coefficient can be used to better understand this strength. It can be somewhat subjective to compare the strength of one association to another. This is true whether the pattern is linear, nonlinear, positive, or negative. The strength of the relationship or association between two variables is shown by how close the points are to each other. This is seen as a linear pattern that falls from left to right. In a negative pattern, as the predictor increases, the value of the response decreases. This shows up in the scatterplot as a linear pattern that rises from left to right. In a positive pattern, as the value of the predictor increases, so does the value of the response. If there is no clear pattern, then it means there is no clear association or relationship between the variables that we are studying.Īs you can see above, linear patterns can be thought of as either positive or negative. Whatever the pattern is, we use this to describe the association between the variables. Scatterplots with a linear pattern have points that seem to generally fall along a line while nonlinear patterns seem to follow along some curve. In general, you can categorize the pattern in a scatterplot as either linear or nonlinear. Each point represents the value of the response for a given value of the predictor. Using this terminology, a scatterplot is used to understand how the response responds to changes in the predictor. Given a scatterplot, the variable on the horizontal axis is the predictor (or independent variable) and the variable on the vertical axis is the response (or dependent variable). Questions like “When the temperature increases, do gas prices also increase?” or “How are changes in the price of gas related to the number of miles people drive each month?” can be answered by studying the pattern in a scatterplot. Essentially, correlation is the measure of how two or more variables are related to one another.Scatterplots are used to understand the relationship or association between two variables.

However, when used in a technical sense, correlation refers to any of several specific types of mathematical operations between the tested variables and their respective expected values. In informal parlance, correlation is synonymous with dependence. However, in general, the presence of a correlation is not sufficient to infer the presence of a causal relationship (i.e., correlation does not imply causation).įormally, random variables are dependent if they do not satisfy a mathematical property of probabilistic independence. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are linearly related.įamiliar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve.Ĭorrelations are useful because they can indicate a predictive relationship that can be exploited in practice. In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. N.B.: the figure in the center has a slope of 0 but in that case, the correlation coefficient is undefined because the variance of Y is zero. The correlation reflects the noisiness and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). Several sets of ( x, y) points, with the Pearson correlation coefficient of x and y for each set. For other uses, see Correlation (disambiguation). This article is about correlation and dependence in statistical data.


 0 kommentar(er)
0 kommentar(er)
